Mengenal Definisi Turunan Fungsi Aljabar (Derivative Algebra Functions)

Memperkenalkan Definisi Turunan Fungsi Aljabar, dalam bahasa inggris mungkin bisa disebut Derivative Algebra Functions.

Secara umum Turunan atau Derivatif dalam ilmu kalkulus merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai masukan. Secara khusus lagi turunan mengukur perubahan fungsi yang sangat kecil atau turunan dapat didefinisikan sebagai perubahan nilai fungsi terhadap perubahan nilai masukan untuk perubahan yang sangat kecil (mendekati nol).

Contoh pengamatan perubahan yang mungkin sudah pernah kita lakukan adalah pengamatan perubahan tinggi kecambah mulai dari hari pertama sampai hari ketujuh. Perubahan tinggi kecambah kita amati setiap hari, artinya tinggi kecambah berubah seiring dengan perubahan waktu dalam satuan hari. Jika perubahan adalah $\delta$, tinggi adalah $h$ dan waktu adalah $t$, maka perubahan tinggi seiring dengan perubahan waktu dapat kita tulis dalam bentuk $\dfrac{\Delta h}{\Delta t}$.

Apabila pada suatu fungsi $y=f \left( x \right)$ yang terdefinisi pada selang terbuka $I$ yang memuat semua bilangan riil. Bila nilai $x$ berubah dari $x_{1}$ ke $x_{2}$, maka nilai fungsi juga akan berubah dari $y_{1}=f \left(x_{1} \right)$ ke $y_{2}=f \left(x_{2} \right)$. Dengan demikian perubahan nilai fungsi terhadap perubahan nilai x didefinisikan sebagai:

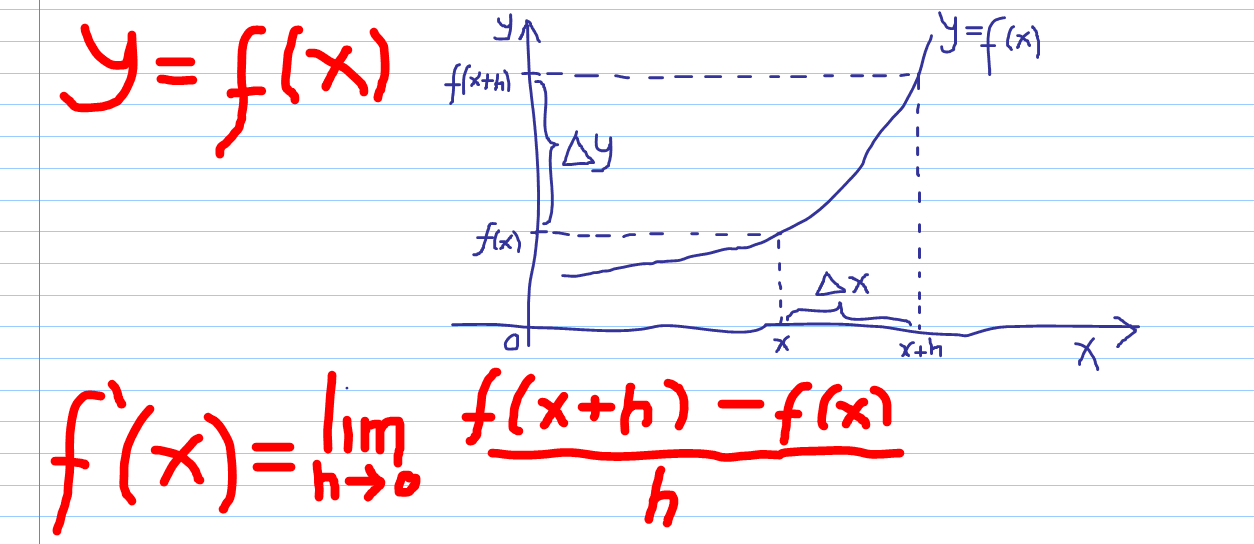
\begin{align} \dfrac{\Delta y}{\Delta x}\ &= \dfrac{y_{2} -y_{1}}{x_{2}-x_{1}} \\ \dfrac{\Delta y}{\Delta x}\ &= \dfrac{f \left(x_{2} \right)-f \left(x_{1} \right)}{x_{2}-x_{1}} \end{align} Misalkan $\Delta x$ sebesar $h$ kita gambarkan dalam grafik koordinat kartesius, ilustrasinya seperti berikut ini:

Perubahan nilai $x$ sebesar $h$ atau $\Delta x=h$, sehingga berlaku $x_{2}-x_{1}=h$ atau $x_{2}=x_{1}+h$. Apabila kita substitusi nilai $x_{2}=x_{1}+h$, maka kita peroleh: \begin{align} \dfrac{\Delta y}{\Delta x}\ &= \dfrac{f \left(x_{2} \right)-f \left(x_{1} \right)}{x_{2}-x_{1}} \\ \dfrac{\Delta y}{h}\ &= \dfrac{f \left(x_{1}+h \right)-f \left(x_{1} \right)}{x_{1}+h-x_{1}} \\ \dfrac{\Delta y}{h}\ &= \dfrac{f \left(x_{1}+h \right)-f \left(x_{1} \right)}{h} \\ \end{align} Untuk $\Delta x$ atau $h$ yang sangat kecil yang mungkin dapat kita sebut mendekati nol dapat kita tuliskan: \begin{align} \lim\limits_{h \to 0} \dfrac{\Delta y}{h}\ &= \lim\limits_{h \to 0} \dfrac{f \left(x_{1}+h \right)-f \left(x_{1} \right)}{h} \\ \end{align} Persamaan di atas disebut dengan definisi dari turunan pertama fungsi $f(x)$ di titik $x=x_{1}$, yang dapat dituliskan dalam bentuk: \begin{align} f' \left( x_{1} \right) = \lim\limits_{h \to 0} \dfrac{\Delta y}{h}\ &= \lim\limits_{h \to 0} \dfrac{f \left(x_{1}+h \right)-f \left(x_{1} \right)}{h} \\ \end{align}

Secara umum definisi turunan fungsi $y=f \left( x \right)$ dituliskan $f'\left( x \right)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$ dengan catatan bahwa nilai limit ini ada. Jika $f' \left( x \right)$ bisa diperoleh $f \left( x \right)$ dikatakan dapat diturunakan (diferentiable).

Turunan pertama suatu fungsi $y=f \left( x \right)$ dapat dinotasikan dengan notasi dari Newton dan Lagrange yaitu $f'\left( x \right)$ atau $\dfrac{d}{dx} f \left( x \right)$ atau notasi Leibniz yaitu $\dfrac{dy}{dx}$.

Sedangkan nilai turunan di suatu titik tertentu (misalnya di $x=c$) dinotasikan dengan $f'(c)$ atau $\left.\begin{matrix} \dfrac{dy}{dx} \end{matrix}\right|_{x=c}$. Notasi $d$ yang dipakai merupakan singkatan dari kata derivative, yang berarti turunan.

Turunan (diferensial) dari sebuah fungsi $f$ adalah fungsi yang dituliskan $f'$ (dibaca"f aksen"). Jika sebuah fungsi dengan variabel $x$ dituliskan $f(x)$ maka turunan pertama fungsi tersebut adalah $f'(x)$, didefinisikan $f'(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$ dengan catatan bahwa nilai limit ini ada. Jika $f'(x)$ bisa diperoleh $f$ dikatakan dapat diturunakan (diferentiable).

Untuk lebih memahami penggunaan definisi turunan fungsi di atas, mari kita lihat beberapa contoh soal berikut:

Dengan menggunakan definisi turunan fungsi, tentukan turunan pertama dari fungsi $f(x)=3x+4$

Sebelum kita menentukan turunan fungsi $f'(x) = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$, tahap awal kita coba tentukan fungsi $f(x)$ dan $f\left( x+h \right)$ yaitu:

$\begin{align} f(x) & = 3x+4 \\ f\left( x+h \right) & = 3\left( x+h \right)+4 \\ & = 3x+3h+4 \end{align}$

Lalu $f\left( x \right)$ dan $f\left( x+h \right)$ kita substitusi ke definisi turunan fungsi, sehingga kita peroleh:

$\begin{align} f'(x) & = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h} \\ & = \lim\limits_{h \to 0} \dfrac{\left( 3x+3h+4 \right) - \left( 3x+4 \right)}{h} \\ & = \lim\limits_{h \to 0} \dfrac{3x+3h+4 - 3x-4 }{h} \\ & = \lim\limits_{h \to 0} \dfrac{3h }{h} \\ & = \lim\limits_{h \to 0} 3 \\ & = 3 \end{align}$
$\therefore$ Turunan pertama $f(x)=3x+4$ adalah $f'(x)=3$

Dengan menggunakan definisi turunan fungsi, tentukan turunan pertama dari fungsi $f(x)=5x-3$

Sebelum kita menentukan turunan fungsi $f'(x) = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$, tahap awal kita coba tentukan fungsi $f(x)$ dan $f\left( x+h \right)$ yaitu:

$\begin{align} f(x) & = 5x-3 \\ f\left( x+h \right) & = 5\left( x+h \right)-3 \\ & = 5x+5h-3 \end{align}$

Lalu $f\left( x \right)$ dan $f\left( x+h \right)$ kita substitusi ke definisi turunan fungsi, sehingga kita peroleh:

$\begin{align} f'(x) & = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h} \\ & = \lim\limits_{h \to 0} \dfrac{\left( 5x+5h-3 \right) - \left( 5x-3 \right)}{h} \\ & = \lim\limits_{h \to 0} \dfrac{5x+5h-3 - 5x-3 }{h} \\ & = \lim\limits_{h \to 0} \dfrac{5h }{h} \\ & = \lim\limits_{h \to 0} 5 \\ & = 5 \end{align}$
$\therefore$ Turunan pertama $f(x)=5x-3$ adalah $f'(x)=5$

Dengan menggunakan definisi turunan fungsi, tentukan turunan pertama dari fungsi $f(x)=7$

Sebelum kita menentukan turunan fungsi $f'(x) = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$, tahap awal kita coba tentukan fungsi $f(x)$ dan $f\left( x+h \right)$ yaitu:

$\begin{align} f(x) & = 7 \\ f\left( x+h \right) & = 7 \end{align}$

Lalu $f\left( x \right)$ dan $f\left( x+h \right)$ kita substitusi ke definisi turunan fungsi, sehingga kita peroleh:

$\begin{align} f'(x) & = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h} \\ & = \lim\limits_{h \to 0} \dfrac{7 - 7}{h} \\ & = \lim\limits_{h \to 0} \dfrac{ 0 }{h} \\ & = \lim\limits_{h \to 0} 0 \\ & = 0 \end{align}$
$\therefore$ Turunan pertama $f(x)=7$ adalah $f'(x)=0$

Dengan menggunakan definisi turunan fungsi, tentukan turunan pertama dari fungsi $f(x)=3x^{2}-5x$

Sebelum kita menentukan turunan fungsi $f'(x) = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$, tahap awal kita coba tentukan fungsi $f(x)$ dan $f\left( x+h \right)$ yaitu:

$\begin{align} f(x) & = 3x^{2}-5x \\ f\left( x+h \right) & = 3\left( x+h \right)^{2}-5 \left( x+h \right) \\ & = 3\left( x^{2}+2hx+h^{2} \right) -5x-5h \\ & = 3x^{2}+6hx+3h^{2} -5x-5h \end{align}$

Lalu $f\left( x \right)$ dan $f\left( x+h \right)$ kita substitusi ke definisi turunan fungsi, sehingga kita peroleh:

$\begin{align} f'(x) & = \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h} \\ & = \lim\limits_{h \to 0} \dfrac{\left( 3x^{2}+6hx+3h^{2} -5x-5h \right) - \left( 3x^{2}-5x \right)}{h} \\ & = \lim\limits_{h \to 0} \dfrac{3x^{2}+6hx+3h^{2} -5x-5h - 3x^{2}+5x }{h} \\ & = \lim\limits_{h \to 0} \dfrac{6hx+3h^{2} -5h}{h} \\ & = \lim\limits_{h \to 0} \left( 6x+3h-5 \right) \\ & = 6x+3(0)-5 \\ & = 6x-5 \end{align}$
$\therefore$ Turunan pertama $f(x)=3x^{2}-5x$ adalah $f'(x)=6x-5$

Jika tertarik untuk membahahas soal-soal tentang turunan fungsi yang sudah pernah diujikan pada Ujian Nasional atau Ujian Seleksi Masuk Perguruan Tinggi Negeri silahkan di simak pada:

• Bank Soal dan Pembahasan Matematika Dasar Turunan Fungsi Aljabar
• Bank Soal dan Pembahasan Matematika Dasar Turunan Fungsi Trigonometri
• Aplikasi Turunan Fungsi (*Soal BSE Matematika SMA Kelas XI IPA)